可以根据问题的不同难度,将问题进行不同的划分:
P 问题(polynomial time)、NP 问题(nondeterministic polynomial time)、NPC 问题(NP complete)、NPH 问题(NP hard)
不可判定问题(undecidable problem)是一类特殊的决定性问题,它的特点是我们无法设计一个算法来求解它的结果。
其中一个比较典型的例子就是停机问题

- P问题
P 取自 polynomial time,指的是可以用确定型图灵机🔍在多项式时间内解决的问题。
也就是我们通常意义下所说的,可以在多项式时间内解决的问题。
注意是可以在多项式时间内解决的问题
- NP问题
这个说法等价于可以用确定型图灵机🔍在多项式时间内验证(判断答案是否正确)。
也就是我们通常意义下所说的,可以在多项式时间内验证的问题。
可以在多项式时间内验证,但是不一定会在多项式时间内解决
- NPC问题
NPC 即 NP complete,NP 完全,是 NP 中最难的决定性问题(并不是无限定词的最难的问题!)。而我们称满足如下条件的问题为 NPC 问题:
- 是一个 NP 问题;
- 所有 NP 问题都可以多项式时间归约🔍为该问题;
归约也就是可以用这个NPC问题的解法来解决其他同样的类似的问题
一旦有一个 NPC 问题被解决,那么所有 NPC 问题,乃至所有 NP 问题都能被解决
如果我们试图证明一个问题是 NPC 问题,我们可以通过这种手段:
- 判定该问题是一个 NP 问题;
- 判定一个已知的 NPC 问题可以多项式时间归约🔍为该问题,或判定该问题是 NPH(在下面)问题;
- NPH问题
NPH 即 NP hard,NP 困难,它不一定需要是 NP 问题。而所有 NP 问题都可以多项式时间归约🔍为 NPH 问题。
也就是说NPC=NP∩NPH
相关的例子
- Halting problem
停机问题是一个典型的不可计算问题,它指的是,对于任意一个程序,我们无法设计一个算法来判断它是否会在有限时间内停机(即判断程序是否会死循环)。
理解上面这段内容的关键就是,这里虽然不存在事实意义上的“死循环”,但可以理解为这里存在一个逻辑上的递归,而这种“逻辑上的递归”,正是导致停机问题成为一个不可计算问题的原因。
- Hamilton Cycle Problem
哈密顿回路问题
给定一个图,判断是否存在一条路径,使得它经过图中的每个点恰好一次,且最后回到起点。
哈密顿回路问题是一个 NPC 问题
- Traveling Salesman Problem
首先TSP是一个NP问题这事容易得到的,但是如何证明他是NPC问题呢,我们需要证明TSP问题也是一个NPH问题,然后取交集部分即可得到
- Circuit-SAT

一个关于停机问题的一个例子:
理发师悖论
克里克岛的一座小城里有位理发师, 有一天他做出一项规定: 他给并且只给那些不给自己理发的人理发. 理发师的这个规定似乎很有道理, 既然有人自己给自己理发了, 那么我就不用"多此一举", 我再给这个人理发.
最初, 这个规定并没什么问题, 后来, 随着这个理发师自己的头发越来越长, 他发现他陷入了一个两难的境地: 他该不该给自己理发?
- 如果他为自己理发. 那么他就成为了他规定中那个"自己给自己理发的人", 那么他就不应该为自己理发;
- 如果他不为自己理发, 那么他不是他规定中那个"自己给自己理发的人", 那么他就应该为自己理发.
综合以上两种情况, "他为自己理发"当且仅当"他不为自己理发", 这成为了一个悖论.
理发师悖论在很多领域有重要的应用, 比如罗素利用理发师悖论发现了集合论的缺陷, 在当时学术界引起了极大震动. 在这里, 我们要用理发师悖论分析停机问题.
除此之外SAT问题,顶点覆盖问题,哈密顿回路问题,TSP问题,团问题,最长路径问题,背包问题都是NPC问题,停机问题不是NPC问题,停机问题是不可判定问题。
- Formal-language Theory
an abstract problem Q is a binary relation on a set I of problem instances and a set S of problem solutions.
对于最短路径问题来说,他的实例就是某个图,他的solution就是某个path,通过最短路径的某个算法把两者关联起来
任何优化问题都可以通过枚举解空间来转化成判定问题。而判定问题的解空间就是0和1,归约要求两个问题的实例解要相等,而判定问题的解都是0和1,所以可以轻易地满足这个条件。

描述P,NP,NPC问题
回过头来看P类问题,给定一个language,如果一个算法能在多项式时间内判定这个语言,那么我就说这是P类语言或者说是P类问题
验证算法是一个双参数算法A,其中一个参数是一个普通的输入字符串x,另一个是一个称为证书(其实就是这个问题的解)的二进制字符串y
如果存在一个证书y,对于某个输入字符串x,使A(x, y) = 1,那么就说验证算法A可以验证这个算法。


NP和NP问题的补,学术界更倾向于右下方的情况,也就是说NP和co-NP问题之前存在交集
如果某个language L1以多项式时间归约到L2,那么我们记作(如图所示)

那么我们要证明一个NPC问题就有两步(第一步是证明这是NP问题,第二部用已知的NPC问题进行归约)
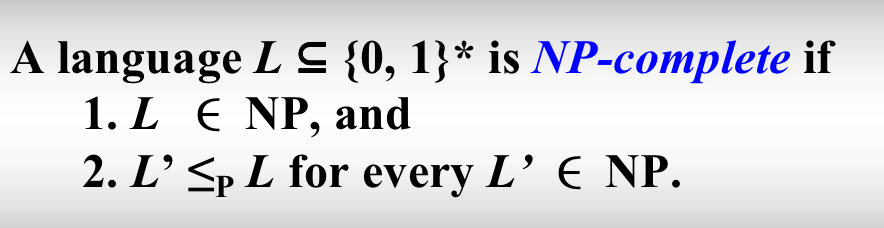
假设我们已经知道团问题是NPC,求证点覆盖问题也是NPC问题。
团问题:给定一个无向图,给定一个正整数K,能否找到一个完全子图(任意两个节点)并且有K个节点?
点覆盖问题:给定一个无向图,给定一个正整数K,能否找到一个节点的子集(个数最多为K)使得任意一条边的某个端点是包含在这个子集之中的?
现在我们要从团问题归约到点覆盖问题来证明点覆盖问题也是NPC问题。